Point Set Topology
During the Fall 2010 semester I taught Math 4200/6200: Point Set Topology; this page contains some of the course information and interesting topics.
End-of-Semester Project Ideas
Students choose one of these and presented the topic to the rest of the class during the last two weeks of the course. This gives students a chance to work with some independence in an area of interest, and gain some experience presenting specialized material.
Metrization Theorems
Urysohn and/or Nagata-Smirnov. This is a major topic, and a critical one. One challenge here is conveying the intuitive idea of the proofs while still giving enough details to make sense. Another challenge is fitting it all into a single talk.Embeddings of Manifolds
This is a fundamental idea for geometry. Munkres Topology has a couple of different embedding results which require only the tools of point set topology. Familiarity with manifolds will help, but is not necessary, and the proof is not particularly long.Critical Examples
An increasing, nowhere-differentiable function, a space-filling curve, the lakes of Wadda, the Alexander horned sphere, and others. Examples like these rock our geometric intuition, reminding us of how wild continuity can be. Cover as many of these as you can, making sure to give the essential details together with the intuitive ideas.Topological Dimension and Fractal Dimension
Explain these quantities and compute some interesting examples. Depending on your interest, you may focus on one or the other of these, proving some of the basic theorems or giving some more sophisticated examples.The fundamental theorem of algebra
This is technically a part of algebraic topology, but only slightly, and it's extremely important! This may require a bit more independent reading, but isn't particularly hard.The category of compactly generated spaces
This is the category which most modern topologists study, and there are a number of reasons it is preferred. These have everything to do with point-set topology, and are described succinctly in Chapter 5 (only 3 pages!) of Peter May's "A Concise Course in Algebraic Topology". Someone particularly interested in topologies on function spaces or categorical properties may enjoy this topic.The Klee Trick
Let \(A\) and \(B\) be two closed embeddings in \(\mathbb{R}^n\) of the same space. Then the pairs \((\mathbb{R}^{2n}, \mathbb{R}^{2n} \setminus B)\) and \((\mathbb{R}^{2n}, \mathbb{R}^{2n} \setminus A)\) are homeomorphic! This implies that \[ H_*(\mathbb{R}^n \setminus A) \cong H_*(\mathbb{R}^n \setminus B). \] Describe the proof of this fact (using the Tietze extension theorem), and give some of the amazing consequences (e.g. all knot complements are homology-equivalent). For this topic, some familiarity with homology is probably necessary, although not much.Other ideas
There are a number of interesting topics in the "Supplementary Exercises" sections, and also in "optional" sections we've skipped -- these could be great topics if they catch your eye.Errata to Topology, 2nd edition, by James Munkres
page number; line number -- starred numbers count from bottom of page.
- xii; 13
- of connectedness and compactness in Chapter 3.
- 107; 2
- f maps [0,1) into S super 1
- 111; 15
- The wording is confusing. Try this: Let X and X' be spaces having the same underlying set; let their topologies be...
- 118;
- Exercise 9, line 2, J is not empty.
- 143; 1
- composite g is ...
- 151; 2*
- (a sub 1, ..., a sub N, 0, 0, ...)
- 187; 4*
- Let A be a subset of X.
- 203; 12
- b < a. Neither U nor V contains a sub 0.
- 203; 15
- U and V not containing a sub 0, but containing
- 205; 9*
- if and only if X is T sub 1 and for every...
- 224; 13
- open in X sub i for each i.
- 235; 13*
- Show that if X is Hausdorff
Note: if X is assumed to be only T_1, then the natural numbers with finite-complement topology provides a counterexample. - 237; 8
- Assume script A is a covering of X by basis elements such that
- 251; 7
- less than or equal to 1/n
- 261; 7
- replace "paracompact" by "metrizable".
- 262; 8
- (x, epsilon sub i)
- 263; 1*
- Throughout, we assume Section 28.
- 266; 8*
- rho super bar is a metric;
- 356; 7
- Find a ball centered at the origin...
- 417; 11
- element of P(W),
- 421; 8
- length (at least 3), then
- 425; 10*
- (G sub 1) * (G sub 2)
- 445; 10
- Exercise 2 should be starred.
- 466; 4
- = (w sub 0)[y sub 1] a [y sub 2] b ...
- 481; 1
- with k(h(e sub 0)) = e sub 0.
- 488; 4
- F = p inverse (b sub 0).
- 488; 11
- of the subset
- 503; 14*
- either empty or a one- or two- point set!
Introductory Pictures
Construction of the Cantor set.

The Serpinski triangle is constructed similarly to the Cantor set.
The Möbius strip has only one side and one edge.

The Hilbert curve is a space-filling curve; this shows one stage of its construction. Here is a logo demo from pappert.
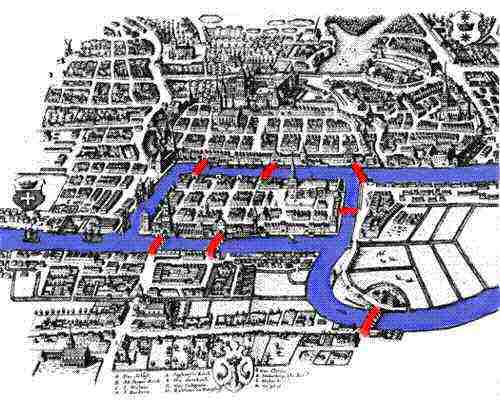
The seven bridges of Königsberg cannot be crossed exactly once in a single trip. (Euler 1735)

universal cover of genus two surface
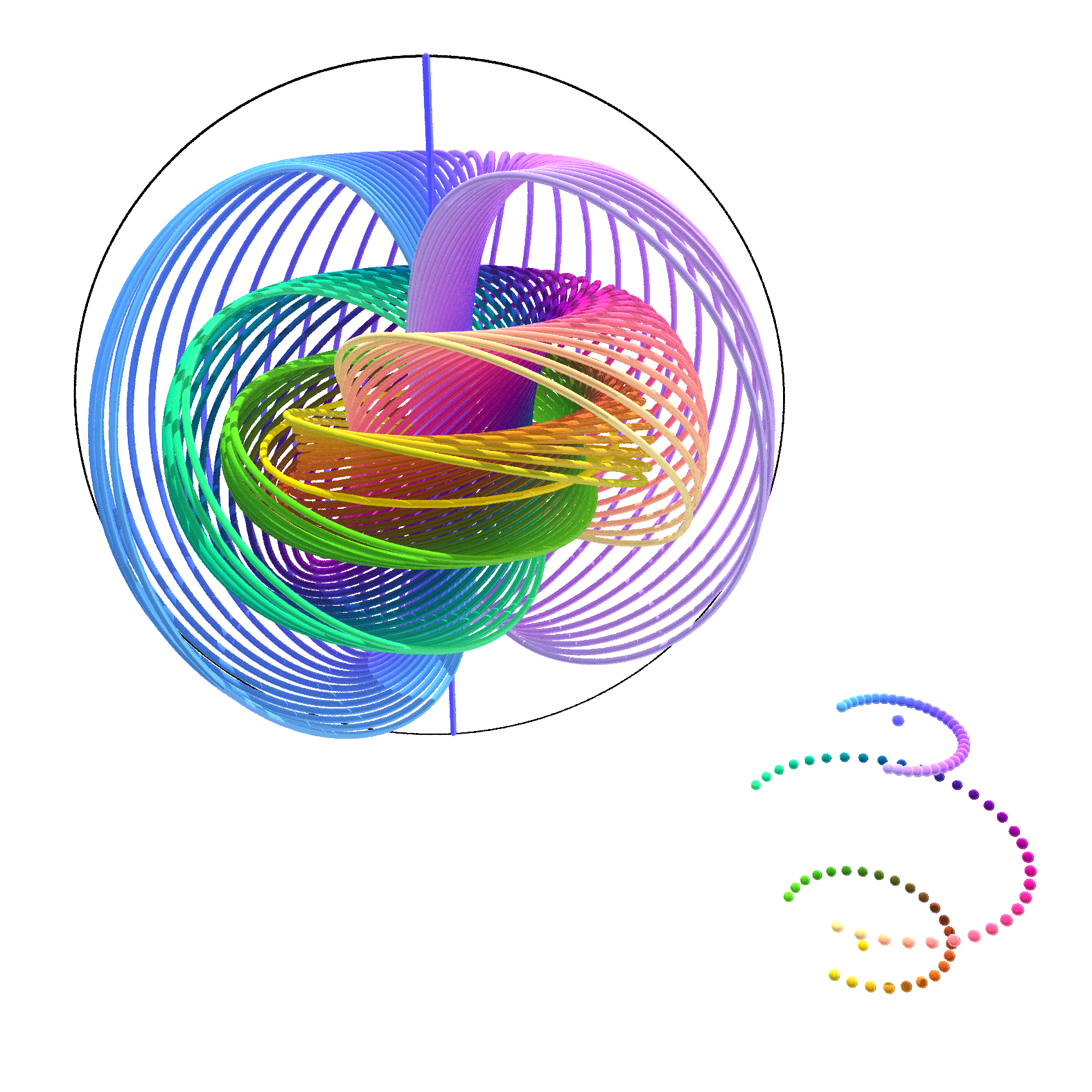
The Hopf fibration is a non-trivial "projection" whose fibers are circles.
tags: fun-topics