This is an archived post from older social media. The original is no longer accessible.

Assuming things go well tonight, we will have an announcement tomorrow . . .

Our announcement is out!

This includes some hard-to-find proofs, with a level of detail that might be considered superfluous by experts. But novices are our target audience. Watch this space for more comments after I’ve had a rest, or just go check it out for yourself.

[2002.06055] 2-Dimensional Categories

Together with Donald Yau, I am happy to announce our new book on 2-/bicategories. The purpose of this book is to provide an elementary introduction to category theory in dimension 2, with complete details of definitions and basic results.

We couldn’t include everything we wanted – there really is too much! But we like what’s in there and we hope you all will too :)

• A chapter on tricategories, and the proof that the totality of bicategories forms a tricategory.

• A final chapter with additional topics: various monoidal bicategories, the Gray tensor product, double categories, and monoidal double categories.

Along with basic definitions, you will find:

• Chapters on the pasting theorem and Whitehead theorem (local characterization of biequivalences).

• A chapter on the bicategorical Yoneda lemma

• Two chapters on the Grothendieck construction

As an aside, I would like to say, loudly and publicly, how much I’ve enjoyed working with Donald Yau. I could not have finished a project like this without his advice, and I’ve learned a lot about what it takes to write a book.

Nothing is ‘easy’: Since our goal is to be as approachable as possible, we avoid words like “easy”, “obvious”, and “clear” as much as we can. Instead of saying something is easy, we say why it’s easy.

For example, we might say something follows by naturality of the associators instead of saying it follows ‘easily’. This is the kind of thing that is easy for experts, and should be! But for beginners it can be mystifying. It really was for me :)

In a more daunting example, one of the details for proving that bicategories form a tricategory is proving that the pseudofunctoriality constraint of horizontal composition is actually a modification. This means showing that a certain square commutes …

Commutativity of that square is “easy” in the sense that it doesn’t involve any clever idea. Just apply the axioms. But doing so requires quite a few steps—51 by our count. So we organize them into 10 subdiagrams (numbered by subscripts) and write them out!

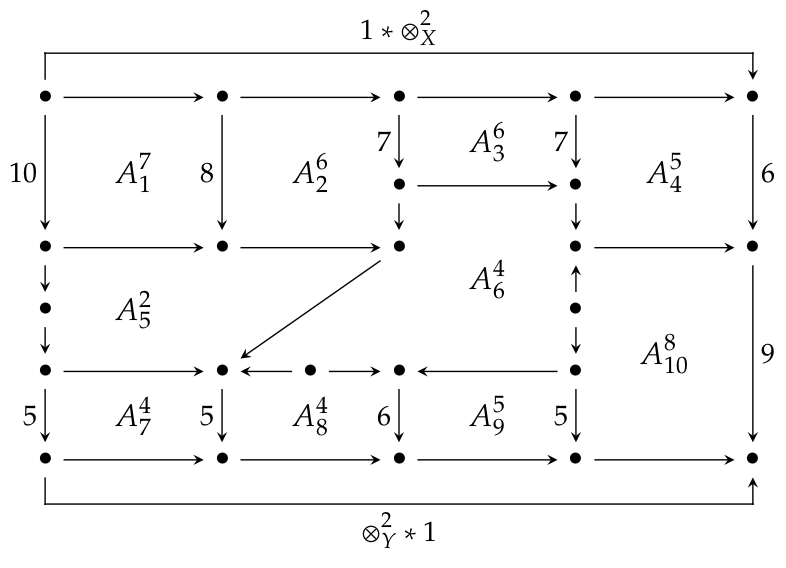
You don’t have to read it if you don’t want to. But if you do want to, we have it there for you :)

Now, we do say things are “left to the reader”, but each of those is written as a numbered exercise and we give them when the key techniques or ideas have already been demonstrated.

For better or worse, you won’t find clever puzzles or novel points of view in the exercises. Instead, you’ll find space to test out the techniques we’ve demonstrated and check your comprehension.

Beauty in clarity: Some of the material has, until now, had me pretty confused. Getting the details straightened out lets the underlying beauty of the subject shine through, and that was a real joy to see.

While working to get the details straightened out, we gained a better perspective on the 1-categorical analogues too. The Yoneda Lemma is a good example. Even the 1-categorical case can be a mind-bender when you first encounter it. We learned to think about it in three parts.

In the rest of the chapter we work through the bicategorical analogue of each part. They all come together in a lovely way!

We emphasize key details in “Explanation” environments; these are things that one needs to work out in order to make sense of later constructions/proofs.

p.s. Before we imply it’s all rainbows and sunshine, I should say: Yes, this material is complicated. So, we’ve done our best, but I think my excerpts here also show that one probably can’t just dive in to the middle and expect to understand what’s going on!

You can think through them, skip them until they’re needed, or skip them altogether if you don’t need that level of detail. Either way, seeing how the details all fit together is one of the most enjoyable parts of doing mathematics, and one we are pleased to demonstrate :)

The other way we try to help is with “Motivation” environments. These usually precede the more complex definitions, to help the reader make sense of what’s coming up, and why.

And lastly, for those who don’t know, I should point out that this Motavation/Explanation structure is one Donald has used in many of his other books, so he is to be credited for the idea :)

tags: social | books