This is an archived post from older social media. The original is no longer accessible.

Announcement time! Donald Yau and I have a new three-volume work. It’s a little too big for the arxiv, so you can download it at https://nilesjohnson.net/En-monoidal or https://u.osu.edu/yau.22/main

The objects of study are ring-like categories, where there is a symmetric monoidal addition and another monoidal multiplication. The multiplication is not necessarily symmetric, and there is a distributivity morphism. For example: direct sum and tensor product of vector spaces!

Volumes I and II (by Donald) describe the different types of symmetry (En-monoidal) that the multiplication might have. Roughly speaking, En-monoidal mult. has the kind of symmetry that multiplication in an n-fold loop space has. There are some very cool applications in there!

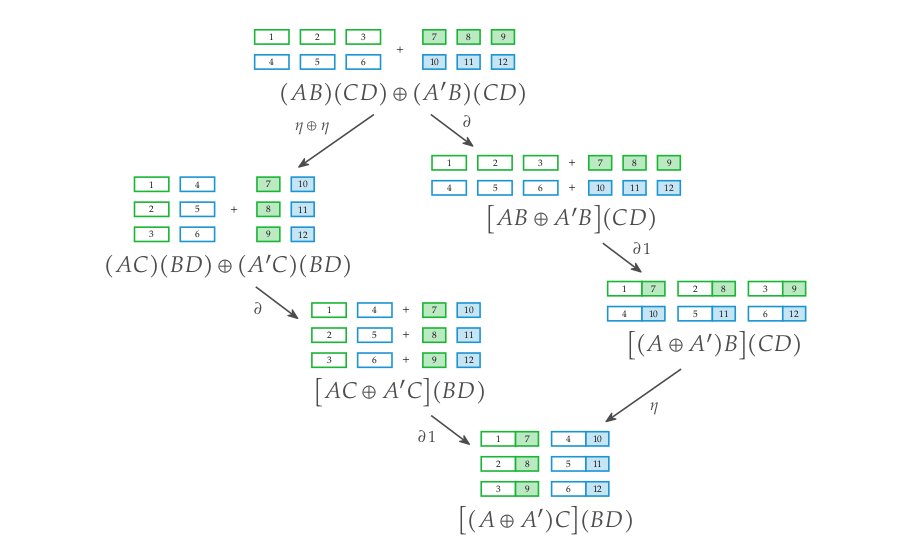
The picture on the cover is a cartoon of one of the distributivity axioms, called Exchange Factorization. To interpret the cartoon, take B=3, C=2, and D=1. A and A’ are the lengths of the strips, and the numbers are there so you can track how the strips are permuted.

The reason that people are interested in En-monoidal categories is that their K-theory spectra have an En-ring structure. That’s the subject of Volume III, and the part I worked on.

Volume III also has a part 1 that goes over all the enriched monoidal category theory that one needs for the K-theory work. If you have heard me complain about math woes on this birdsite, it’s been about that part! But it also has a lot of really lovely diagrams :)

It turns out to be quite a bit of enriched category theory, and you can read it independently of the rest of the book(s). We cover strictification/coherence for enriched monoidal categories, (conical) enriched co/ends, the enriched Yoneda lemma, and Day convolution.

There’s a lot more to say—around 1400 pages more—so I’ll just stop with one cute bit of algebra that is independent of the rest (but absolutely crucial). The partition multicategory encodes the algebra of partitions for a finite set…

You can start with the commutative monoid of subsets, with their union, but for partitions you need to restrict to only allow unions of disjoint subsets. This makes the algebra more like addition of numbers, and it’s key to the K-theory applications. Note the Mod^M1 there…

M1 is the partition multicategory for the 1-element set! It’s not that complicated, but we ended up needing to say a lot about it.

All of this builds to some pretty neat applications, constructing En-monoidal structures for spectra.

For a more thorough overview, check out our Preface, or list of Main Facts. We also have an appendix of open questions that we wondered about but had to leave unexplored.

Lastly, I have to add how much I enjoyed working with Donald again. Especially during the disaster of the past year (going on two). I’m at a complete loss for words to describe it, so I’ll just say he’s been great :)

tags: social | books