Tensor products for permutative categories
Note: This was first posted as a mathstodon thread, and archived here.
Our paper on tensor products for permutative categories is now online!
Why are you running away?! It's actually very nice!
https://arxiv.org/abs/2211.04464

A giant martian crab, with a strangely dismayed frown, grabs some of the tiny people running around its feet. Both the crab and the people look more confused than angry or scared. It's cover art, by Paul Lehr, from a 1969 book The Nets of Space, by Emil Petaja.
The title of this paper is a bit tricky, because (it's been known for a long time) permutative categories do not have a symmetric monoidal tensor product. Not symmetric monoidal as a category. But, what we show, is that it is symmetric monoidal as a bicategory. And, we include enough details so you can see just where the difference occurs.

The paper has a lot more. It includes many of the basic things that go along with tensor products, and the details of how they work in this setting. If you're really into that kind of thing, I think you'll find it useful!
Here, I just want to add a couple of weird/neat things: (1) coproducts via the Gray tensor product; (2) subtleties about the monoidal unit.

(1) The direct sum (coproduct) of permutative categories comes from the Gray tensor product! For permutative categories A and B, you can form one-object 2-categories ΣA and ΣB. Then their Gray tensor product, ΣA ⊠ ΣB, is another 1-object 2-category, and it has a permutative category C of 1- and 2-cells.

That permutative category C is the direct sum A ⊕ B. We also give a straightforward objects-and-morphisms definition, but I think the connection with the Gray tensor product is neat. This direct sum is equivalent (not isomorphic) to the cartesian product!

(2) The monoidal unit, S, is also known as the natural number category. It's objects are natural numbers, and it's morphisms are given by permutations of n-elements sets. A subtle but apparently important fact is that the 2-unitors are not strict.


This seems related to corresponding monoidal unit subtleties for (a) EKMM S-modules, where S is the sphere spectrum, and (b) Elmendorf-Mandell M1-modules (in pointed multicategories). We don't have a mathematical statement of this relationship, just a feeling we can't put into words.
Thanks for reading! If you want to know more, go check that paper out. It's long, but the details are relatively straightforward. We tried to organize it so thoroughly that people can find what interests them with relative ease. An appendix about symmetric monoidal bicategories marks all the data that are trivial (or not) for permutative categories! A coherence theorem makes checking the nontrivial part pretty easy.
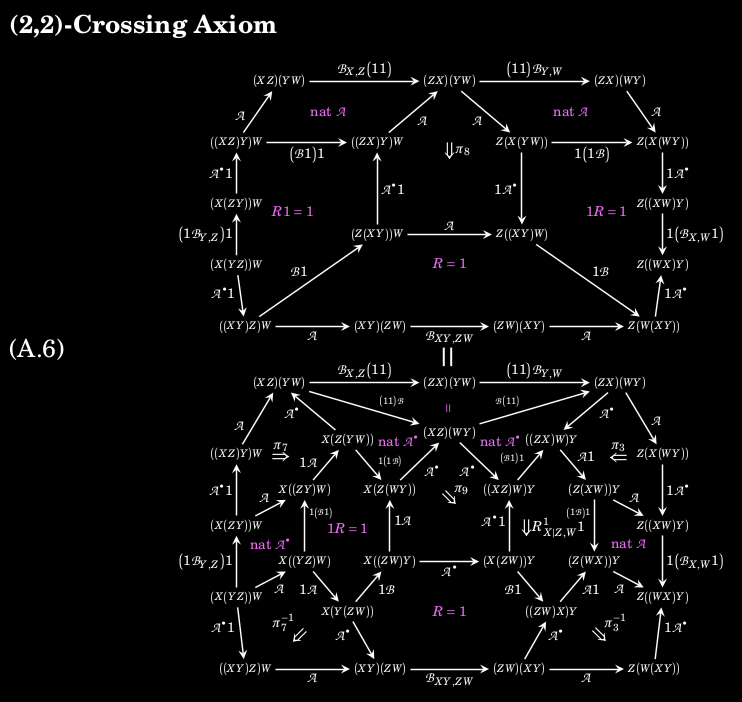
(I think this diagram looks a little like a giant crab face.)
Here's what I was trying to convey about the diagram looking like a crab.
Overlay of the top part of the (2,2)-crossing axiom over the giant Martian crab from the first post. The outline of the diagram aligns very roughly with the crab body, and the one nontrivial 2-cell is over the frowning crab maw. Two arrow labels A happen to fall over the googly crab eyes.