Constructing Spectral Sequences
While teaching Homological Algebra, I had the occasion to give an introduction to spectral sequences. The approach I took was similar to that of McCleary:
McCleary,
A User's Guide to Spectral Sequences.
Cambridge studies in advanced mathematics, 58. 2001.
I gave a fast description of what a spectral sequence is, and then focused on various techniques by working through illustrative examples over the next week. After we had done several examples, I wanted to go back and show my students the construction of a spectral seqeunce from a filtered chain complex. My first attempt at this turned out to be confusing and poorly presented—I believe I effectively communicated how easy it is to get lost in indexing and subquotients of subquotients!
To make a better second attempt, I looked for an outline and illustration of the construction. Not finding one, I produced the following picture. I made scans of three stages in the drawing, so that I could make slides showing successive layers of the picture. I then filled in notes explaining the picture, and decided to share them here.
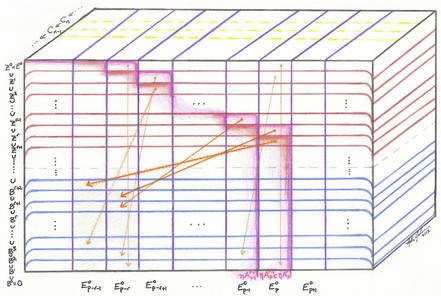
A schematic illustration showing various terms arising in the construction of a spectral sequence for a filtered chain complex.

Slides and notes
I hope you enjoy the slides and notes, but let me apologize in advance: These are not written for novice users. They focus exclusively on the construction of a spectral sequence, assuming that the reader is familiar with the goals of this construction. There are many good resources which describe how to use spectral sequences, and which give motivation for why they are useful. These notes do not attempt to address either of those important questions.
Our goal is to give a visual aid to complement the standard construction of a spectral sequence for the homology of a filtered chain complex. The notation follows §5.4 of Weibel:
Weibel,
An introduction to homological algebra.
Cambridge studies in advanced mathematics, 38. 1994.
As Weibel does, we drop the complementary degree q for readability.
- Slides present the illustration in three layers, with more information on each successive layer.
- Notes to accompany the slides, including explanatory remarks not written on the slides. The notes contain a larger version of the final illustration, but leave out the earlier stages for ease of printing.
tags: fun-topics | mathart